The implementation of DepEd’s K-12 program is underway and has started taken effect since last school year in the Philippines. In line with this, private schools are making or have already announced adjustments in their curriculum to comply with the government’s K-12 program. Some schools will move their grade 7 program to their HS department, others did bridging programs this summer. On the other hand, some schools opted for mass acceleration or re-labeling of student levels (Grade 1 students last year will be in Grade 3 this coming school year). Although the over-all goals of K-12 education are laudable, students in transition will have to go through a period of adjustment especially in subjects, such as Math, where topics and skills build on previous knowledge and experience.
Is your child ready for the K-12 transition in Math? Math skills are cumulative and a strong foundation goes a long way in ensuring continued confidence and success. Math skills such as critical and analytical thinking, problem-solving skills take time to master. One way to determine your child’s math competence is to do an assessment. The assessment test will identify the student’s strengths, gaps and weaknesses in math concepts in the previous grade. Knowledge and skill gaps can be addressed this early to ensure a smoother transition to the k-12 program and life long success for your child.
(photo from www.specialeducationphilippines.com)
Singapore math is the term used by countries other than Singapore to refer to its Math curriculum as developed by Singapore’s Ministry of Education. In Singapore, this is simply referred to as “Maths curriculum” (yes, its Math with an “s” following the British English standard which shortens Mathematics to Maths instead of the western shorthand Math). The curriculum contains the framework for understanding, learning and teaching mathematics which aids teachers in delivering quality math teaching as well as specific sequences of topics from Primary 1 to 6. Mathemagis’ Singapore Math program is aligned with Singapore’s effective framework of math learning and pedagogy.
Below is a summary table which shows a comparison of the Singapore Math to traditional Math approaches.
| Traditional Math | Singapore Maths |
|---|---|
| Teaches the “hows” (how to add, subtract, multiply, etc) | Teaches the “whys” before the “hows” (why do we borrow? Why do we carry in addition? Why is 4 x 3 = 12? Why is there a remainder?) |
| Focuses on mathematical procedures and formulas | Focuses on conceptual understanding of topics so students understand how the procedures came to be and help them discover the formulas on their own. |
| Proceeds immediately to abstract ideas (use of symbols and jargon like ‘+’, ‘lcd’, ‘n’) | Moves from a concrete then to a visual/pictorial presentation of concepts before introducing abstraction |
| Covers topics on the four operations, fractions, decimals, ratio, percentage, area & perimeter, measurements, geometry & word problems | Covers topics on the four operations, fractions, decimals, ratio, percentage, area & perimeter, measurements and geometry & word problems |
| Uses purely equations to solve word problems | Uses the bar-model approach in solving word problems to develop students’ visualization skills (beginning at the 2nd grade) allowing them to solve complex word problems without using algebra when they reach the 4th grade |
| Mastery of procedures achieved through repetition and drills alone | Mastery of math concepts achieved through a gradual and logical progression of topics on top of exercises with emphasis on word problems |
| Goal is fast, and accurate computations | Goal is to develop analytical thinking skills through an understanding of math concepts and visualization |
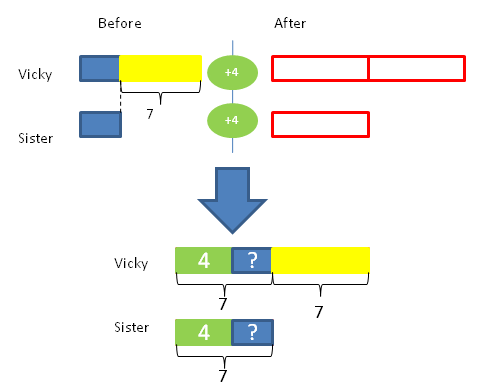
Below is a word problem given in a 4th Grade Singapore Math Contest in Metro Manila.
Vicky is 7 years older than her sister. In four years time, Vicky will be twice as old as her sister. How old is Vicky’s sister at present?
For parents, the first thing that comes to mind is to use algebra. Most likely, one would remember encountering this kind of age problem in his/her first year high school algebra class using the traditional curriculum. Presently, schools using the traditional curriculum cannot give this kind of problem to 4th graders because they will need algebra to solve it. However, students using Singapore math can solve this problem using the bar-model approach. Here is the solution.
The model shows the before (Vicky is 7 years older than his sister) then the after four years scenario where Vicky is twice as old as her sister. Finally, the combination model systematizes all the givens. First, “four years from now” is represented as the additional (4) in the right side. Second, Vicky’s age is twice her sister’s age. Third, Vicky is still 7 years older than her sister (please note that Vicky will always be 7 years older than her sister). Now we have three equal parts. Since one part is equal to 7, each of the two equal parts is also seven. Therefore, 7 – 4 = 3. Vicky’s sister is 3 years old at present.
To check, if the sister is 3 years old at present, then Vicky is (7+3 = 10) 10 years old. Four years from now, Vicky will be (10+4 = 14) 14 years old which is twice the age of her sister (3+4 = 7) who will be 7 years old four years from now.
Although the computation involved is quite simple (7–4 = 3) that even a 1st grade student can solve it, the modeling requires thoughtful visualization, analysis and knowledge of before-and-after, multiplication, part-whole and adding-on model concepts learned from the 2nd to 4th grades.
When learned properly, the power of the bar model lies in its ability to help students visualize and draw complex word problems as well as the corresponding solutions without the need for complex algebraic equations.