Jan
4
In Mathemagis, we believe that everyone can be good in Maths. With our visual approach and emphasis on developing analytical skills for word-problem solving, your child can surely achieve success this year and beyond. Start the year right and visit us for a free assessment.
Dec
15
Mathemagis adopts Singapore’s National Institute of Education’s (NIE) Teacher Education Model for the 21st century (TE21) particularly the V3SK model of combining Values, Skills and Knowledge in molding teachers who are equipped not just with Singapore Maths knowledge but are armed with pedagogical skills and empowered by student-centered and professional values.
Dec
7
Mathemagis Singapore Maths focuses on developing students’ problem-solving skills through conceptual understanding of math principles instead of rote memorization of procedures, visualization strategies instead of abstract explanations, use of bar-models to help students organize and break-down complex problems and fostering algebraic-thinking skills instead of short-cut methods. Students get the best foundation for learning higher math such as algebra, trigonometry and calculus.
This approach allows 6th grade students to confidently answer word problems in College entrance exams without the need to learn algebra. Imagine what they can do in high school! Let your children amaze you with their problem-solving skills with Mathemagis’ Singapore Math. Call us now for a free assessment.
Below is an example of a standard 6th grade word problem in ratio:
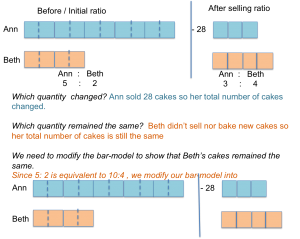
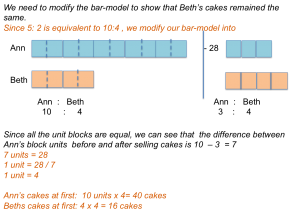
The ratio of the number of cakes Ann baked to the number of cakes Beth baked was 5:2. After Ann sold 28 cakes, the ratio became 3:4. How many cakes did each girl have at first?
Jan
23
Mathemagis’ Singapore Math covers core content areas of Math learning and skills development.
1. Conceptual Understanding
Students learn the whys before the hows and understand the underlying mathematical principles behind common shortcuts and formulas. An emphasis on conceptual understanding allows students to solve seemingly complex problems with ease.
Traditional Math: 5 x 3 = ?Singapore Math: 5 x 3 = 5 x 2 + ?
Level 2 (grade 2) students will be able to answer this based on a conceptual understanding of multiplication (no algebra, please).
2. Procedural Mastery
Knowledge and mastery of mathematical procedures are developed AFTER conceptual understanding.
3. Mental Computations strategy
Students learn various mental computation strategies on top of pen and paper calculations.
4. Use of Bar model in word problems.
Students develop visualization and analytical skills needed to learn higher mathematics such as trigonometry and calculus through the use of bar-models as early as level 1 (grade 1).
Traditional Math Algebra Word Problem : Jose’s present age is 1/7 of his father’s age. His father will be 61 years old in 5 years’ time. In how many years’ time will Jose’s age be 1/5 of his father’s age?Singapore Math Level 5 (Grade 5) Word Problem: Jose’s present age is 1/7 of his father’s age. His father will be 61 years old in 5 years’ time. In how many years’ time will Jose’s age be 1/5 of his father’s age?
Level 5 students will be able to answer the above problem using the bar-model approach. Yes, without using algebra! Singapore math focuses on visualization, analysis and strategies for breaking down complex word problems — allowing grade 5 students to answer questions normally reserved for Algebra.
5. Heuristics
Mathemagis teaches various strategies that can be applied to word problems aside from the bar-model approach. This makes students more versatile and exposed to a wide range of word problems both mathematical and practical.
The Mathemagis Singapore math program covers all content areas and skills development in mastering primary school math and preparing students for higher order math such as Algebra, Trigonometry and Calculus.
Aug
5
No. Some problems do not lend themselves to bar-modeling. Singapore Math teaches various strategies, called heuristics, for solving these kinds of so-called non-routine word problems. There are about nine heuristics used in Singapore Math. These strategies are taught as early as Primary 1 and spirals through Primary 6.
How does a student know when to use the bar-model and when to use heuristics? There are no hard and fast rules on when to use a specific strategy in problem solving. However, exposure to a variety of word problems, hours of practice and proper teaching methodology help, of course. In the end, the goal of Singapore math is to arm the students with various strategies to solve a variety of word problems and to develop analytical skills to decide which strategy is most applicable in a given problem or situation.