Below is a word problem given in a 4th Grade Singapore Math Contest in Metro Manila.
Vicky is 7 years older than her sister. In four years time, Vicky will be twice as old as her sister. How old is Vicky’s sister at present?
For parents, the first thing that comes to mind is to use algebra. Most likely, one would remember encountering this kind of age problem in his/her first year high school algebra class using the traditional curriculum. Presently, schools using the traditional curriculum cannot give this kind of problem to 4th graders because they will need algebra to solve it. However, students using Singapore math can solve this problem using the bar-model approach. Here is the solution.
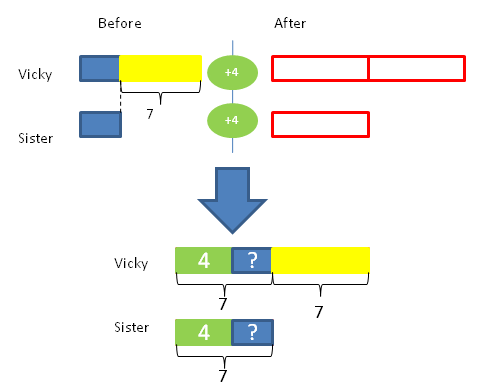
The model shows the before (Vicky is 7 years older than his sister) then the after four years scenario where Vicky is twice as old as her sister. Finally, the combination model systematizes all the givens. First, “four years from now” is represented as the additional (4) in the right side. Second, Vicky’s age is twice her sister’s age. Third, Vicky is still 7 years older than her sister (please note that Vicky will always be 7 years older than her sister). Now we have three equal parts. Since one part is equal to 7, each of the two equal parts is also seven. Therefore, 7 – 4 = 3. Vicky’s sister is 3 years old at present.
To check, if the sister is 3 years old at present, then Vicky is (7+3 = 10) 10 years old. Four years from now, Vicky will be (10+4 = 14) 14 years old which is twice the age of her sister (3+4 = 7) who will be 7 years old four years from now.
Although the computation involved is quite simple (7–4 = 3) that even a 1st grade student can solve it, the modeling requires thoughtful visualization, analysis and knowledge of before-and-after, multiplication, part-whole and adding-on model concepts learned from the 2nd to 4th grades.
When learned properly, the power of the bar model lies in its ability to help students visualize and draw complex word problems as well as the corresponding solutions without the need for complex algebraic equations.